Predikce zásob pomocí AI
3. Jak to validovat
Základní otázka před jakýmkoliv tréninkem
Smyslem validace je ověřit, jak si model poradí s daty, která nikdy neviděl – stejně, jako v reálném provozu. Proto je nutné dataset rozdělit na dvě části:
- Tréninková data – na nich se model učí.
- Validační (testovací) data – na nich se kontroluje, co model opravdu umí.
Ale kde stanovit hranici?
Chtěl jsem modelu poskytnout všechny možné informace – všechny SKU a všech 36 měsíců – abych zachytil co nejvíce vzorců. Část časové osy však musela zůstat skrytá; jinak by si síť jednoduše zapamatovala historii a v realitě se zhroutila.
Řešení? Vytvořil jsem tři validační scénáře, které postupně zvyšují přísnost: od „rychlé zkoušky“ (model validuje pouze na datech, jež už viděl) až po ostrý test jen na opravdu neviděných měsících.
3 scénáře validace
- Scénář 1: Pro základní testování jsem nejprve použil validaci nad stejným datasetem jako byl trénink (tj. celé období 36 měsíců).
Cílem bylo ověřit, jestli je model vůbec schopen najít vzory a predikovat hodnoty, které už viděl (je zde riziko přetrénování modelu). - Scénář 2: Trénink na omezené historii (33 měsíců), validaci na posledních 6 měsících (3+3, 3 měsíce, které model při tréninku viděl a 3 nové měsíce).
Tento postup už mnohem lépe simuluje reálné nasazení: model nejprve „projde historií“, naučí se z ní vzory a teprve poté predikuje nové, neznámé období. Díky tomu lze:- Prověřit schopnost generalizace – jestli model umí správně extrapolovat trend, nebo jen opakuje to, co už zná.
- Odhalit posun v sezonních vzorcích – například zda si poradí s vánoční špičkou či jinými vzory.
- Odhalit vliv sale akcí – jestli výsledné predikce jsou ovlivněny plánovanými slevovými akcemi
- Citlivost na nové položky – poslední měsíce často obsahují zboží s krátkou historií; validace tak rovnou ukáže, jak si model poradí se sortimentem, který se průběžně mění.
- Scénář 3: Stejný trénink jako ve Scénáři 2, Validace = pouze poslední 3 měsíce (tedy data která neviděl). Tento scénář jsem používal jako kontrolní validaci.
Až když jsem byl s výsledky spokojený, natrénoval jsem finální verzi na celém datasetu (bez vyčleněné validace), aby model využil 100 % dostupných dat pro ostré nasazení ve skladu.
Poznámka: Všechny metriky a grafy, které dál v článku ukazuji, pocházejí ze Scénáře 2 (pokud výslovně neuvedu jinak). Metriky jsou tedy počítány na posledních 3+3 měsíců. Vizualizace pro názornost zobrazuje 12 měsíců.
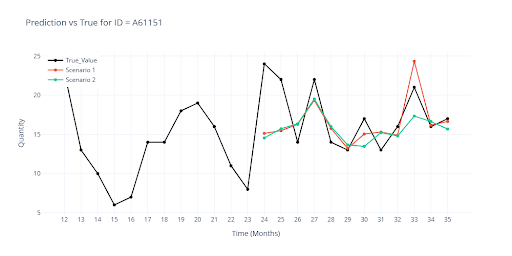
Následující graf ukazuje rozdíl mezi scénářem 1 a 2. Červený graf ukazuje Scénář 1, tedy kdy model při tréninku viděl všechny výsledky.
Zelený graf je Scénář 2, kdy poslední 3 měsíce nebyly součástí tréninku. Je zřejmé, že je nutné do validací zahrnout hned od začátku neviděná data.
Jakou metriku tedy vybrat, když není technicky možné ručně zkontrolovat každé zboží?
V praxi je běžné používat například R², RMSE nebo MAPE – proč tedy vůbec vymýšlet něco jiného? Zásadním problémem je existence nul a vysoká variabilita hodnot.
Proč jsou nuly problém?
Představte si, že model predikuje pro daný měsíc obrat 2 kusy, zatímco reálný prodej byl nula. Zdánlivě chyba jen 2 kusy, ale pokud použijeme procentuální metriku (například MAPE), vyjde nesmyslně vysoká chyba, protože se dělí nulou nebo velmi malým číslem.
Podobně je tomu u RMSE – pár „menších” odchylek na položkách s velkými prodeji může nafouknout celkovou chybu a zcela zastřít výkon modelu na hlavních položkách.
Proč je vysoká variabilita hodnot problém?
| Příklad položky | Reálný obrat | Predikovaný obrat | Absolutní chyba | Relativní chyba |
|---|---|---|---|---|
| A (nízký obrat) | 5 ks | 8 ks | 3 ks | 60% |
| B (vysoký obrat) | 5 000 ks | 4 800 ks | 200 ks | –4 % |
- MAPE bude vysoké kvůli položce A (60 %), i když reálně jde o ±3 kusy.
- RMSE naopak zvýrazní položku B (200 ks), protože je výrazně citlivý na velké absolutní chyby.
- R² může vypadat výborně (99 % rozptylu vysvětleno) díky položkám s vysokými prodeji, ale pro „malé“ položky je tato metrika často málo vypovídající.
Jedna metrika nestačí.
Vysoká variabilita položek, hodně nulových a malých položek.
Musel jsem přistoupit ke kombinaci více metrik.
| Metrika | Co vlastně měří | Poznámka | Cíl |
|---|---|---|---|
| WAPE (Vážená procentní chyba) | Kolik % celkových prodejů model „netrefil“. | Citlivost na sortiment s nulovým obratem. | ⬇️ |
| RMSE (Prům. absolutní chyba) | O kolik kusů se v průměru netrefíme. | Citlivost na sortiment s velkými obraty. | ⬇️ |
| R² (Koeficient určení) | Jak velkou část pohybů v prodejích model správně „vysvětluje“. | Hodně ovlivněn velkými obraty. | ⬆️ |
| MAPE (Průměrná absolutní procentuální chyba) | Průměrná procentní chyba každé položky. | Citlivost na sortiment s nízkými obraty. | ⬇️ |
| Robust score | Kombinace přesnosti, kontroly odchylek a shodu směru trendu. (1 = skvělé, 0 = špatné) | Zachytí stoupající/klesající trend. | ⬆️ |
| Stable score | WAPE + kontrola odchylek a relativní chyby u drobných prodejů. (nižší = lepší) | Zajišťuje, že predikce je hladká a stabilní měsíc po měsíci a není náchylná na sortiment s malými obraty. | ⬇️ |
Cíl označuje, jaké hodnoty potřebujeme (nízké ⬇️ nebo vysoké ⬆️).
Jako hlavní metriky používám WAPE, RMSE a R².
- MAPE metrika není vhodná pro variabilní položky.
- Robust a Stable používám zejména pro ověření základní koncepce modelů. Pro drobné ladění se tyto hodnoty výrazně nemění.
Moc jednoduché?
V průběhu tréninku jsem narazil na další problém v aplikaci metrik. Standardní metriky přes celý dataset jsou velmi vypovídající, ale neupozorňují na odchylky u jednotlivých položek. Z toho důvodu jsem rozšířil použité metriky na:
| Verze metriky | Jak se počítá | Na co odpovídá |
|---|---|---|
| Výpočet za celý dataset | Hodnoty ze všech položek se sloučí do jednoho vektoru a z něj spočítám metriky. | Kolik kusů se netrefí v celkovém objemu? Tedy finanční dopad na skladové zásoby. |
| Výpočet po položkách | Metrika se spočte pro každé zboží zvlášť, potom se z těchto čísel udělám průměr. | Jak přesná predikce je u typického produktu? – tedy kvalita napříč celým sortimentem. |
Příklad vypočtených metrik nad modelem s 2 vrstvami neuronových sítí a softplus normalizatorem. Významné jsou zde rozdíly mezi metrikami WAPE a MAPE. Druhá tabulka ukazuje správně natrénovaný model.
| Metrika | Hodnota (ALL) | Hodnota (Item) |
|---|---|---|
| WAPE | 50.1925 | 387.2097 |
| RMSE | 69.0821 | 31.4245 |
| R² | 0.6239 | |
| MAPE | 107.1253 | |
| ROBUST | 0.455 | 207.7031 |
| STABLE | 0.5869 |
| Metrika | Hodnota (ALL) | Hodnota (Item) |
|---|---|---|
| WAPE | 31.1611 | 44.6504 |
| RMSE | 50.2607 | 26.5974 |
| R² | 0.9084 | |
| MAPE | 75.7044 | |
| ROBUST | 0.5226 | 84.916 |
| STABLE | 0.3901 |
Vizuální pozorování
I přes kombinaci metrik jsem v průběhu testování zjistil, že vizuální kontrola je nutná.
Zejména u zboží s určitým rozložením hodnot, jako jsou speciální typy prodejů, mnoho nulových hodnot a sezónní prodej, jsou metriky nevypovídající – špatné výsledky se v množství schovají.
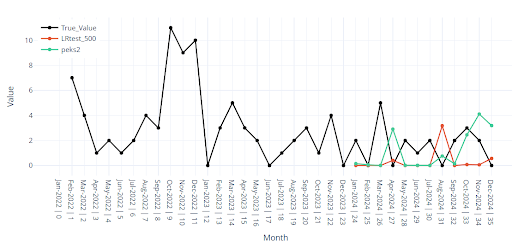
Následující příklad ukazuje tento případ. I když jeho metriky nevypadají špatně, tak predikce pro poslední měsíce je téměř nulová (červená). Tento případ nastává velmi často právě o zboží s velmi nízkými prodeji.
| Metrika | Hodnota (ALL) | Hodnota (Item) | Hodnota (ALL) | Hodnota (Item) |
|---|---|---|---|---|
| WAPE | 41.2218 | 61.4738 | 34.7262 | 51.7859 |
| RMSE | 67.3586 | 29.0839 | 48.2791 | 23.7958 |
| R² | 0.7453 | 0.8691 | ||
| MAPE | 82.3626 | 70.7658 | ||
| ROBUST | 0.4432 | 88.1001 | 0.4785 | 77.5447 |
| STABLE | 0.4872 | 0.418 | ||
| Červený graf | Zelený graf | |||
Poznámka: Ve vizuální validaci je vždy reálný prodej zobrazen černou barvou a predikce barevně.
